Anti-aliasing in Reaktor, Part I

This tutorial covers what aliasing is, what causes it, and why we wish to avoid it. I’ll introduce some basic concepts that we will use in later tutorials to create efficient, fully band-limited oscillators with no aliasing artifacts.

This tutorial builds off of material first introduced in the Additive Synthesis series, which you can access here. If you don’t know what a harmonic is or how the Sine Bank module works it may be a good idea to read parts I + II of that series before continuing.

DIGITAL AUDIO AND ALIASING

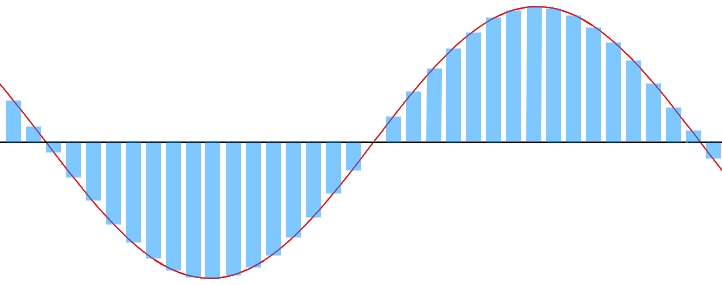
While analog waves have a continuous form, digital ones do not:

The red line in the above image represents an analog sine wave. The blue rectangles represent what the analog signal looks like when digitally sampled.

Digital sampling works fine as long as the signal you are sampling (or creating, as is often the case in Reaktor) has a frequency less than the sampling rate / 2. This limit is referred to as the Nyquist frequency. If the signal contains frequencies greater than the Nyquist, you will create audio artifacts called aliasing.

Now, since the audio sampling rate in Reaktor is usually 44.1 kHz by default, and since human hearing cuts out entirely around 20 kHz (less than the Nyquist, of course), you might be thinking that this problem will never affect you – after all, you don’t want to create frequencies beyond the limit of human hearing anyway!

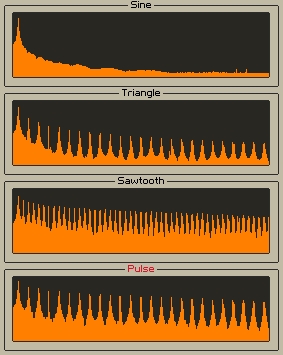
That was my line of thinking when I first learned about aliasing. Unfortunately, it’s not that simple. Have a look at this graph, which displays the spectral components of some common waveform types, all generated using Reaktor Primary modules:

The graph shows the amplitudes of a 440 Hz signal at frequencies ranging from 0 to the Nyquist (22.05 kHz).

As you can see, only sine waves are ‘pure’. All other wave types contain harmonics, the square and saw waves worst of all (for more on the topic of harmonics check out the Additive Synthesis tutorials).

These harmonics stretch well beyond the Nyquist frequency. This means that if you use the Primary Sawtooth and Pulse Oscillator modules like I did to make these graphs, you will create aliasing artifacts!

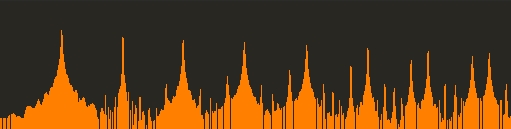
Here’s a spectral graph of a Sawtooth Oscillator module played at a higher frequency:

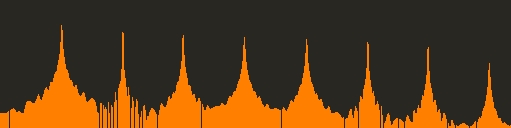
And here’s what a band-limited sawtooth looks like at the same frequency:

You can see all of the extra unwanted spectral information in the aliased waveform. Fortunately, most of the aliased components will be masked by the rest of the sound since they have less amplitude. What happened to these harmonics? The following equation gives the relationship between the digital frequency (F dig), the ideal, analog frequency (F ana), and the Nyquist (N):

The equation works for analog frequency values ranging from 0 to the sampling rate. Beyond that, the pattern simply repeats. A simple example would be that if you have a Nyquist at 10 kHz, and you try to play back a sine wave at 11 kHz, it instead plays back a wave at 9 kHz. Clearly this is undesirable. For a visual representation of how this happens, this page contains some pretty useful images.

BAND-LIMITED OSCILLATORS

A band-limited oscillator is an oscillator that contains no harmonics above the Nyquist. The trick is to create a wave that looks and sounds as much like a sawtooth, triangle or pulse wave as possible, while eliminating unwanted components above the Nyquist.

There are many ways of doing this. Typically, the easier the method, the less efficient it is! A great example of this is using additive synthesis. In an earlier tutorial on additive synthesis, I showed that it is very easy to coax a Sine Bank module into making an approximation of a sawtooth wave. In fact, a Sine Bank will do this pretty much by default.

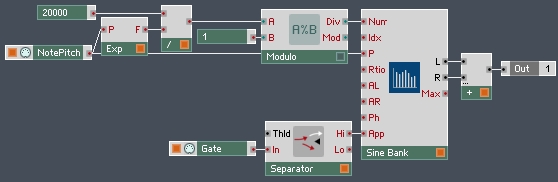
Here’s how one can make a fully band-limited sawtooth using a Sine Bank:

Pretty simple, right? The upside of this design is that it creates a perfectly band-limited sawtooth wave, and is extremely simple both to make and to understand – we simply make a sawtooth out of it’s sine wave components, being careful not to specify any components above the Nyquist. This creates a wave that contains most, if not all, of the audible information of an analog sawtooth.

Unfortunately, there is a problem with this design. Each harmonic is an integer multiple of the base frequency. So, to play a note at 1 kHz, requires that the Sine Bank uses only 20 partials (since our maximum frequency is 20 kHz), which is relatively cheap. However, if you play a note at 50 Hz, you need 20,000/50 = 400 partials!

This results in the oscillator being highly inefficient when playing back lower frequencies. A four voice oscillator with this design takes 1.6% of my CPU to play back the note C4 on every voice. It takes 7.5% to play note C2 on each voice, and a whopping 32.5% to play back note C0! Clearly this won’t do.

However, just because using additive synthesis is a bit too processor intensive for a finalized product doesn’t make it completely worthless. We can still use this oscillator as an example of a perfect sawtooth to measure our future efforts against. Ideally we would like to create an oscillator with the same spectral qualities, that uses a constant amount of CPU. Fortunately, this is a solved and well-documented problem.

In the next tutorial in this series, I will cover some more useful band-limited oscillators and show how to implement them in Reaktor. I hope you have found this to be useful, I will do my best to answer any questions in the comments!